References
- Bing Maps Tile System (http://msdn.microsoft.com/en-us/library/bb259689.aspx) - Describes the tiling system and gives C# code for converting between coordinate systems.
- Virtual Earth Deep Zooming (http://www.silverlightshow.net/items/Virtual-earth-deep-zooming.aspx) - Among other things it describes the URL format for tiles.
- Calculate distance, bearing and more between two Latitude/Longitude points (http://www.movable-type.co.uk/scripts/latlong.html)
- Geographic coordinate system (http://en.wikipedia.org/wiki/Geographic_coordinate_system) - Expressing latitude and longitude as linear units
- Ricky's Bing Map Blog (http://rbrundritt.spaces.live.com/) - Almost everything you would ever need to know about working with Virtual Earth with examples and math.
Why? Because in the technology you are using a map component does not exist, or you are unable to use the existing map component for some reason.
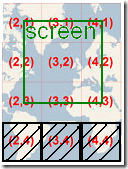
Coordinate Systems There are several coordinate systems involved with using a tile service like Virtual Earth. Virtual Earth and other tile services divide the world in to fixed size tiles at different zoom levels denoted by z, where the number total number of tiles is 22z. The map in this example is at zoom level 3 so there are 64 tiles total, and is derived from the images in Virtual Earth article in the Microsoft Bing Help Docs (http://msdn.microsoft.com/en-us/library/bb259689.aspx).
The world geographic coordinate system (represented in black) is in latitude and longitude and runs from approximately 85 to -85 latitudes and -180 to 180 longitudes. Due to the way the earth in compressed in a tiled map, the lines of latitude are now evenly spaced even through they are the same pixel distance apart. This requires a formula to be used to determining latitude that takes into account this difference.
The tile coordinate system (represented in red) is in row and column, and describes the position of tiles on the world map. All tiles are of a fixed size, though typically at a size of 256 pixels as in the example map, and run from top left to bottom right. Positions in between the upper left corners of tiles are represented using decimal values, so for example (1.5, 0.5) would be in the exact center of tile (1.0, 0.0).
The world pixel coordinate system (represented in blue) is in x and y, and runs from top left to bottom right. It is used to describe the tile coordinate system where tile (0, 0) corresponds to pixel (0, 0). The map size in pixels is ts(2z),where the tile size is denoted as ts and is 256 while z denotes the zoom level and is 3 in the case of the example map.
The screen pixel coordinate system (represented in green) is in x and y, and describes the position of the screen (actually the component displaying the map) in relation to the world map. Because at most zoom levels the world map in pixels is larger than any monitor can display, only the portion of the map which can be seen within the map component is rendered. This means that the size of the component being displayed is dynamic and dependent on the specific application’s usage, as well as how the local x and y relates to the global x and y of the world pixel coordinate system.
General Formulas and Notations
The following is a list of several commonly used formulas and terms.
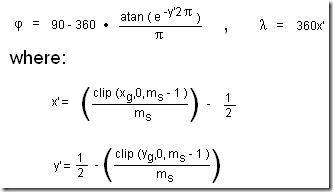
Latitude and longitude to row by column
This formula is used to turn a latitude and longitude form the world geographic coordinate system into a and row by column value in the tile coordinate system.
World x and y to latitude and longitude
This formula is used to convert and x and y position in the world pixel coordinate system to a latitude and longitude in the world geographic coordinate system.
Requesting Tiles
Tiles are requested based on retrieving them one at a time from a URL. How a URL is generated depends on the particular tile server and in the case of this map component only the Virtual Earth tile servers are used. The URL is used to specify the type of image, its zoom and location, and its file type. All files types in Virtual Earth are of PNG or JPG, and the location must be given using the quad key. The quad key is a compressed representation of the tile location using the row, column, and zoom.
The following shows how to generate a quad key using the row, column, and zoom using a Java-like syntax:
String tileToQuadKey(int r, int c, int z) {
String quadKey = "";
for (int i = z; i > 0; i—) {
char digit = '0'; int mask = 1 << (i - 1);
if ((c & mask) != 0)
digit++;
if ((r & mask) != 0) {
digit++; digit++;
}
quadKey += (digit + "");
}
return quadKey;
}
Tile Request and Display Optimization
Only the tiles which are within view of the screen (component) need to be displayed, which means that those should be the only ones to be requested. Once a tile is displayed in order to cut down on loading and rendering time the map component stores the tile, and when it is no longer in view keeps the tile in memory but removes it from the display. For example if the map is to be centered at the tile location of (3.5, 3.5) and is component displaying the map is only large enough to display half of each surrounding tile, than only 9 tiles need to be requested.
In the event that the screen moves up into the next row of tiles the tiles that are now in view should be requested and displayed, while the three tiles that are no longer displayed should be cached.
In order to know which tiles to display and where a center coordinate must be known. Given that center coordinate and the size of the area that will display the map, the tiles to be displayed and their position within that component can be determined.
Determining the tiles to be displayed in the current screen using a center coordinate
Given a coordinate in latitude and longitude to be the center on the map to be displayed, that coordinate can be converted to a tile location in row by column. By using that row and column the range of tiles to be retrieved and displayed can be determined using the amount of space available on the screen and the tile size. The row and column minimums and maximums denote the range of tiles to be displayed, and the delta x and y are used to calculate the pixel distance from the center of the center tile to its upper left corner. This is used to determine how many tiles can fit above, below, to the right of, and to the left of the center tile according to its current position in the center of the screen.
For example if the center coordinate translated to (c, r) = (2.5, 4.5 ) at zoom level 3 and the screen was 512 by 512 pixels, then the column and row minimums and maximums would be calculated as approximately the tiles needed to cover the size of the current screen.
Positioning tiles relative to center
With the range or rows and columns for all tiles to display, given the row and column of a tile its local position in x,y is calculated in the following way:
The x,y local of the tile of the given row and column is calculated relative to the position of the center image. This is done so that panning movement can be calculated relative to the center position of the screen, in order to calculate a simple offset that can be applied to all tiles in order to handle map panning. For example if the center tile location was (c,r) = (2.5, 4.5) and the screen was 512 by 512 pixels, the position of the tile at (c,r) = (1, 3) relative to the center tile would be at (x,y) = (-256, -256).
Handling Map Panning
The end result is that the user should be able to click and drag the map in order to move it around (or to pan). This requires keeping track of where the mouse was clicked, where it was dragged to, and when it was released (to stop worrying about where it is being dragged). During a drag the difference between the current mouse location and the location of the original click can be calculated, and then used to determine the new offset to apply to the map along with the new visible rows and columns.
The variables such as the x,y and r,c min and max values need to be kept track of through the map component life cycle. This is because positioning is done using an offset based on the starting location of the center tile. The offset is calculated using the inverse of the change in mouse position during the click and drag. For example if the user clicks on the map and drags right, more of the map needs to be proportionally drawn to the left. The x and y min and max are used to track the size of the tile area in pixels, in order to determine the how many more tiles are needed at the new map boundaries in terms of rows and columns.
The following shows how the variables in the map panning equation are changed when the screen view (512 by 512 pixels) is moved up on the map by 256 pixels:
Zooming in on a Set of Locations
A function available within most maps is the ability for the map to determine the zoom level to best fit a series of points, and center appropriately. This is generally done by determining the area required in order to display a number of points, and determining the closest matching meters/pixels zoom level and then centering appropriately.
Determining the geographic display area
The geographic display area is determined by taking the minimum and maximum latitudes and longitudes of the list of geographic position, which can be used to construct the geographic positions denoted as A,B, and C. Note that this method for determining geographic bounds will not work across the corners of the map.
Calculating the distance between two geographic points
After determining the geographic display area that is required in terms of the rectangle ABC, the distance from geographic coordinates A to B and B to C needs to be calculated. This requires the ability to calculate the distance between two geographic coordinates, which is described in the following as the function d(A, B):
Calculating the Desired Meters per Pixel
With the the ability to calculate the distance between geographic coordinates, the size of the geographic area to be zoomed in on can be calculated by determining the meters per pixel required to cover the area. This formula assumes a fairly square screen, because it takes the largest distance and meters against the smallest pixel length of the required screen area.
For example using the distances AB and BC, since AB is the largest it is used to calculate the meters per pixels required to display all of the points within the area of rectangle ABC with center G.
Finding Zoom Level based on Meters Per Pixel
(Table from http://msdn.microsoft.com/en-us/library/bb259689.aspx)












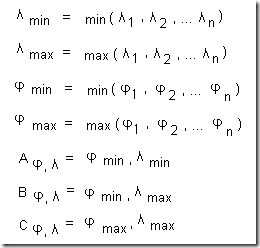




10 comments:
hi.
thanks for wonderful article, i just have question, can you please explain more this paragraph:
"
Due to the way the earth in compressed in a tiled map, the lines of latitude are now evenly spaced even through they are the same pixel distance apart. This requires a formula to be used to determining latitude that takes into account this difference.
"
thanks.
Shlomi
In the first picture in this article the world map is divided into squares with their mappings to the lat-lon, row-column, and x-y systems. Notice how all of the squares are the same size in terms of pixels (256 by 256). Then notice that the degrees of longitude (the widths) of each square is 45 degrees, but that the degrees of latitude (the heights) are not evenly spaced. For example the square at 0,3 is 40.98 degrees in height and 256 pixels in height, while the square at 0,2 is 25.53 degrees in height and 256 pixels in height.
The "Latitude and longitude to row by column" and "World x and y to latitude and longitude" equations are used to convert between longitude-latitude, row-column, and x-y. These equations take into account that degrees of latitude are not evenly spaced.
Ok.. now it's more clearly and i assume this is the reason that the world's height i between 85.X to -85.X degrees but whats happened between this and 90 on north (or -90 on south)? i mean, the coordinates (geo) [90, 180] or [-90, 180] or [90, -180] or [-90, -180] are exists somewhere?
OK.
now, if it's ok, i have another 2 questions:
1. why it's like that, mean, why the latitudes are decreased when you going north and south from the equator?
2. why the world is a square and not oblong, from my prior understanding, the world height should be half then it's width to the whole world should be oblong.
my system already consider the world as oblong, is this mandatory to consider it's as a square?
Hi again,
i have another question:
for the calculation of "Positioning tiles relative to center", you're using O(x,y), what's you meant by: ".. which is (0,0) until a pan"?
it's for tiles that not nearby the local center image?
TA.
Shlomi
Yes, this is the reason for the clipping of the world's height. Those locations do exist at the north and south poles; you just can't view them accurately on a tile based 2D system.
1. why it's like that, mean, why the latitudes are decreased when you going north and south from the equator?
This is because a 3D spherical space was projected into a 2D rectangular space, which means that compression had to occur somewhere. For more information see read this article on "Map Projection": http://en.wikipedia.org/wiki/Map_projection
2. why the world is a square and not oblong, from my prior understanding, the world height should be half then it's width to the whole world should be oblong.
This is how a tile system like Virtual Earth or Google Maps works. Why? Historically it was easier for people to store physical 2D maps on paper rather than as a series of 3D globes. As for why not 2D oblong, see the WIki page on "Map Projection."
According to the "General Formulas and Notations," O (x, y) is used to represent the offset from the center tile image in the local coordinate system. This position is 0,0 until the map is moved. Since this is the local coordinate system once the map is moved, say 10 pixels fo the right, that would make the offset -10, 0.
This is just one of many ways to place tiles and calculate how to move them. Using matrices would be the preferred mechanism; I just found relative geometry a bit more approachable for most people.
"... According to the "General Formulas and Notations .."
so the O(x,y) is accumulate all of the drags that occur from the first time you loaded the map system?
"... he offset from the center tile image in the local coordinate system..."
but when you drag, the 'locally center tile' is changed all the time and not stay the same like 1st one that was on the system loading, for instance, let's say that on the system loading the 'locally center tile' was (3,3) and you dragged the map to another position that now the 'locally center tile' is (6,6), what will be the O(x,y) value (approximated)? the accumulation of all the way till (6,6) or you zeroing it sometimes?
thanks.
Shlomi.
John.
i have another question about the distance calculation (meters/pixel).
as i understood, the meter per pixel value is reduce once you go up and down from the equator, so let's say i have a building (for instance) with 20 meters * 20 meters dimensions, if the building located on the equator (latitude 0) it's should looks realistic but if it's located on lower or higher latitude it'll distort since the meters per pixel there is smaller.
For example, if 20m on the equator are taken 20 pixels (again, for instance) on top or bottom of the world you should represent 20m with higher amount of pixels, am i right?
Post a Comment